張明德, 蔡漢水, 謝樂, 羅沖
重慶理工大學 機械工程學院, 重慶 400054
摘要: 為提高航發葉片前后緣加工精度和加工效率,通過對當前航發葉片前后緣磨削加工中存在的問題進行分析,結合當前葉片前后緣加工工藝要求及數控砂帶磨床各軸運動控制算法,考慮到磨料粒度、接觸力、砂帶線速度及進給速度等磨削要素的影響,優化了刀具軌跡,提出了葉片前后緣磨削工藝方法。最后,對某公司生產的航發葉片進行了磨削加工實驗,實驗結果表明,此磨削加工方法可使得航發葉片前后緣的加工精度和表面粗糙度得到明顯的改善。
關鍵詞:航發葉片 前后緣 運動控制算法 磨削要素 工藝方法
航空發動機葉片(簡稱航發葉片)前后緣對航空發動機的推力、燃油效率、使用壽命等性能指標都起著關鍵作用[1-3]。航發葉片作為形狀復雜的薄壁零件, 葉片前后緣圓弧曲率變化極大、加工余量分布極不均勻, 極易造成前后緣過磨現象, 使得葉片達不到實際加工要求[4-5]。因此, 研究航發葉片前后緣數控砂帶磨削技術對提高航發葉片加工質量及效率具有重要意義。
目前, 國內外有不少學者和技術人員研究葉片數控砂帶磨削技術并取得了較好的應用成果[6-7]。李小彪等[8]為實現砂帶拋光力的實時控制及提高航發葉片表面自動化拋光質量, 提出了航發葉片砂帶拋光力控制技術; 黃云等[9]通過比較國內外砂帶磨削技術的差距, 提出了包括新型砂帶研制、高端精密高效砂帶磨床研制等促進我國砂帶磨削技術發展的新技術; Sarma等[10]針對數控磨削加工道路軌跡生成進行了研究, 提出了一種綜合考慮制造與測量的軌跡生成方法, 使得表面粗糙度的加工前預測成為可能。以上學者對葉片型面的加工工藝進行了深入的分析, 為解決以葉片為代表的自由曲面砂帶精密磨削提供理論支持, 但上述研究目前處于理論研究階段, 尚未應用于實際加工[11-12]。
為解決航發葉片前后緣加工質量問題, 本文在以上研究的基礎上, 展開航發葉片前后緣數控砂帶磨削關鍵技術研究, 并通過磨削試驗驗證其方法的可行性, 得到較好的前后緣輪廓度及較高的表面質量, 并提高了前后緣的加工效率。
1 葉片前后緣磨削工藝分析
數控砂帶磨削加工作為航發葉片前后緣最終成形的一種加工方式, 不僅要有效的提高前后緣的粗糙度, 更要滿足前后緣輪廓度及表面加工質量。隨著航空發動機性能指標的提高, 航發葉片的加工已由單一的尺寸精度要求, 發展為尺寸和表面質量并重的精密加工要求。新型航發葉片采用超音速、三元流設計, 葉片前后緣形狀由圓弧狀發展為高階拋物線形。葉片前后緣的輪廓精度和尺寸精度要求更加嚴格, 通常要求前后緣尺寸精度為-0.03~+0.05 mm, 表面粗糙度小于0.35 μm, 且不接受偏頭、方頭、尖頭、縮頸等不規則形狀(如圖 1所示)。但是, 由于模具的變形與磨損、銑削加工時切削力的變化、裝夾誤差等加工誤差的存在,葉片前后緣加工余量易出現分布不均勻的現象(如圖 2所示), 對數控磨削加工造成了相當大的困難。若采用目前恒定參數的磨削加工方式, 易出現無效與過量磨削, 導致加工效率低, 甚至出現葉片前后緣超差報廢的現象。
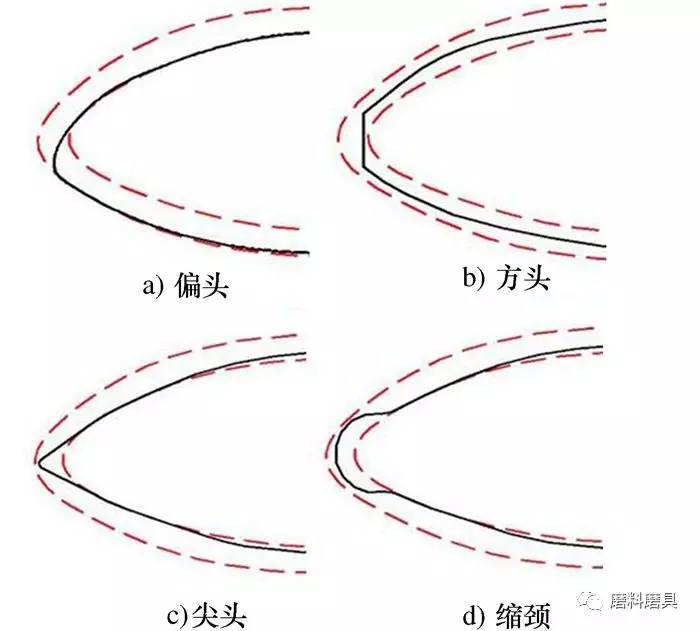
圖 1 典型的航發葉片前后緣不規則形狀
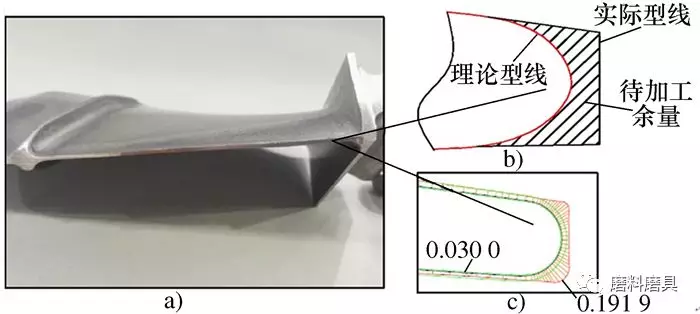
圖 2 航發葉片前后緣余量示意圖
為解決航發葉片前后緣余量分布不均勻的磨削技術難題, 提出了葉片前后緣數控砂帶磨削加工方案。首先, 根據三坐標測量數據, 進行相應軟件開發, 實現航發葉片模型重構; 通過與理論模型進行對比得到刀觸點處加工余量; 其次基于所得加工余量信息, 優化加工余量分布, 考慮磨料粒度、接觸力、砂帶線速度、進給速度等磨削要素的影響, 建立材料去除模型; 基于數控砂帶磨床的結構與各軸運動控制算法, 實現磨削數控程序的編制; 最后, 完成航發葉片前后緣加工成型。
2 航發葉片模型重構與余量提取
對于曲面較為復雜的航發葉片而言, 在逆向過程中, 不同的測量方法往往對應著不同的曲面重構方法。首先采用如圖 3所示的三坐標測量機, 對待加工航發葉片進行測量, 得到各截面線上有規律的離散點云數據, 以C++編程語言為工具, 通過曲面重構算法, 擬合得到非均勻有理B樣條曲面。并通過對比實測模型與理論模型, 求取刀觸點處的加工余量。

圖3 三坐標機測量
2.1 模型重構
目前, 在模型逆向重構工程中, B樣條曲線曲面由于具有幾何不變性、保凸性、局部支撐性及變差減小性等優點而被廣泛采用[13-15]。其中, 非均勻有理B樣條非均勻性是指其節點參數沿參數軸的分布是不等距的; 有理性是指其控制曲線上的權因子可以取不同的值。因此, 其具有統一表達自由曲線曲面和解析曲線曲面的優點。與低次B樣條曲線相比較, 高次B樣條曲線的光滑性較高, 如m次B樣條曲線可以保證m-1階的連續, 但曲線與特征多邊形的逼近程度較差。由于高次B樣條曲線非零區間的擴大, 局部性的優點將逐漸減弱, 而且冪次越高, 計算量也越大。故采用三次非均勻有理B樣條曲線曲面算法進行模型重構。
三坐標測量機采集的點云中, 共有r+1條截面線, 每條截面線有s+1個數據點, 有(r+1)×(s+1)個控制頂點陣列Vi, j(i=0, 1…r; j=0, 1, …s), 即可構成一張特征網格。則有一張3×3次張量積非均勻有理B樣條曲面
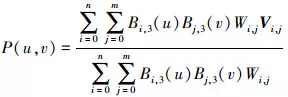 (1)
(1)
式中:r=n+3+1;s=m+3+1;Vi,j為控制頂點; Wi, j為權因子; Bi, 3(u)和Bj, 3(u)分別為沿u向和v向的3次B樣條基函數。
通過讀取三坐標測量機采集的原始數據, 得到一系列封閉的離散點集。并對各截面離散點集進行擬合, 生成一系列三次非均勻有理B樣條曲線, 為提高重構的精度, 有目的地離散各截面曲線, 得到新的點集, 并根據新的離散點集實現曲面重構, 圖 4為利用葉片截面檢測數據擬合的非均勻有理B樣條曲面模型。
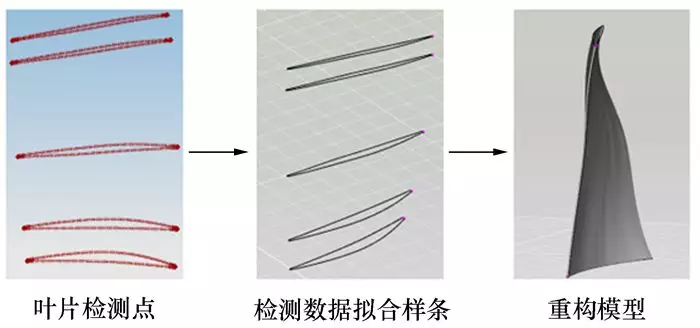
圖4 三坐標機測量點云重構曲面
2.2 刀觸點余量計算
在實際加工過程中, 不同特征的零件以及加工要求的不同, 都會導致加工軌跡方式的不同。根據航發葉片的曲面特征及加工要求, 一般采用參數線法進行磨削加工。將uv參數曲線離散化, 在理論模型上獲得刀觸點坐標, 將實測模型與理論模型進行匹配, 再通過求取葉片理論模型上待加工區域的刀觸點沿法矢方向到重構模型的距離來獲取葉片加工余量。
通過比對葉片型面上的邊、角及孔等特征確定大致的旋轉及平移參數, 再對比葉片型面上的點集, 計算位置偏離, 獲取精確地旋轉參數矩陣R及平移參數矩陣T。為此, 可建立數學模型如下:
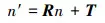 (2)
(2)
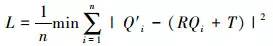 (3)
(3)
式中:n′為重構曲面上的特征點; n為理論曲面對應點; Q′i (i=1, 2, …, n)為重構曲面上的點集; Qi為理論模型上的對應點集。
在理論模型取得n個刀觸點Pi及對應法向矢量n i, 構造沿法矢方向直線Li為
 (4)
(4)
式中ξ為直線參數。
直線與實際模型的曲面相交于一點Qi, 交點與刀觸點之間的距離即為余量Wi。
 (5)
(5)
最后, 對比重構曲面與理論模型計算余量得到如表 1所示結果, 并得到余量分布圖如圖5所示。
表1 理論與實測模型刀觸點及對應余量計算


圖5 某型號葉片加工前后緣區域余量分布圖
3 磨削算法研究
基于上述研究, 根據所得到的待加工葉片刀觸點處的加工余量, 對于磨削算法進一步優化, 實現對航發葉片前后緣磨削加工, 從而提高加工精度和生產效率。
3.1 磨削機床結構與各軸運動
如下圖 6所示, 為某七軸聯動數控砂帶磨床機構原理示意圖, 該砂帶磨床主要結構有:機床床身、立柱、磨頭機構以及各運動控制軸部件等組成。為實現磨削拋光加工要求, 機床要實現如下運動:機床左右、前后、上下方向的直線運動(X、Y、Z軸)、繞X、Y、Z軸方向的旋轉運動(A、B、C軸)、伺服電機對接觸輪的壓力調節(N軸), 同時采用磨頭單懸臂的結構方式。
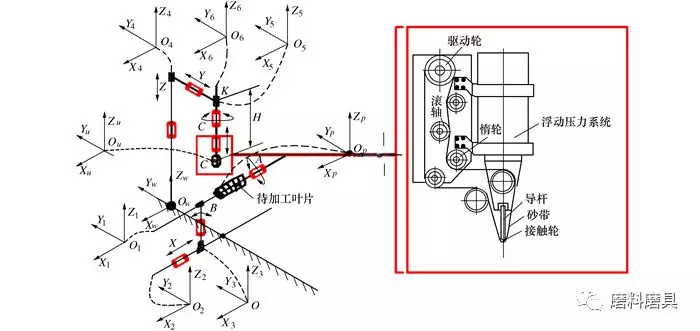
圖6 七軸聯動數控砂帶磨床結構原理圖
該機床主要針對砂帶磨削加工,采用雙擺頭的砂帶磨削機構保證磨頭的支撐方向和葉片曲面的法矢方向一致、使得磨頭的接觸輪軸線和葉片刀觸點的主曲率方向一致, 從而得到磨削加工的最佳位姿。
以葉片理論型面為基準, 建立工件坐標系OpXpYpZp, 與機床坐標系OwXwYwZw保持相同姿態, 獲取曲面各點的坐標和法矢, 用矩陣表示分別是P0=[X0, Y0, Z0, 1]T,N0=[Nx0, Ny0, Nz0, 0]T。若設定刀具初始姿態向量為W0=[0,0,0,1]T, 為滿足C軸回轉軸線與葉片型面刀觸點處法矢同向, 需使工件所處裝夾卡盤繞X軸旋轉A角, 繞Y軸旋轉B角, 如圖 7所示。
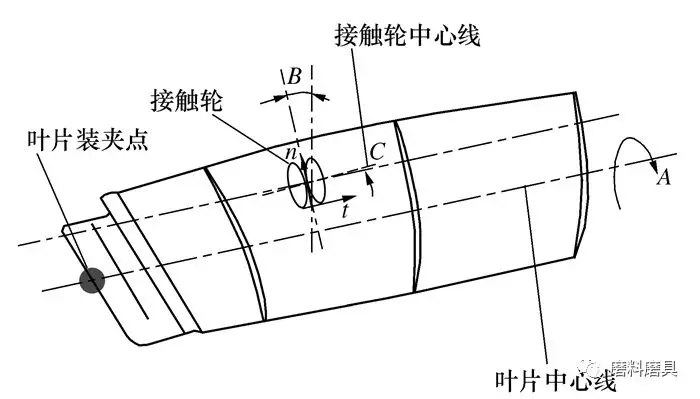
圖7 數控機床回轉軸動作調整過程
其中,
 (6)
(6)
因此, 可以得到A、B兩角的求解公式。
為獲取B角數值, 需要知道葉片繞X軸旋轉A角后, 刀觸點處的法矢N1在工件坐標系OpXpYpZp下所處的姿態。由此可知, N1=Rot(X, A)×N0, 聯立公式可得
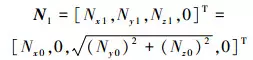 (7)
(7)
由C軸回轉軸線與葉片型面刀觸點處法同向可知,
 (8)
(8)
若設定初始狀態下接觸輪軸線的姿態為T0=[1,0,0,0]T, 刀觸點處切矢的姿態為U0=[Ux0, Uy0, Uz0, 0]T。要滿足接觸輪軸線與葉片型面刀觸點處主曲率方向同向, 必須使接觸輪繞Z軸旋轉一個C角。因此, 需要知道葉片繞X軸旋轉A角和繞Y軸旋轉B角之后, 刀觸點處切矢在工件坐標系OpXpYpZp所處的姿態U1。由此可知,U1=Rot(Y, B)×Rot(X, A)×U0。因為刀觸點處的法矢n與切矢τ垂直, 而且刀具軸線垂直于XOY平面, 所以, 當刀觸點處的法矢n與刀具軸線平行時, 切矢τ一定位于XOY平面內。由此U1=[Ux1, Uy1, Uz1, 0]T=[Ux1,Uy1, 0, 0]T。
那么
 (9)
(9)
刀具按照預定的軌跡進行運動在一定程度上能保證葉片加工精度, 同時也有助于磨削效率的提高。因此, 精確計算出刀觸點投影變換后的坐標值顯得尤為重要。由于A軸和B軸的運動, 葉片型面上各點在工件坐標系OpXpYpZp中位置也會發生相應的改變。首先, 求解出旋轉后葉片上各點在工件坐標系OpXpYpZp的坐標值, 用矩陣表示為P1=[X1,Y1, Z1, 1]T。然后, 建立工件坐標系OpXpYpZp與機床坐標系OwXwYwZw之間的關系, 經過坐標變換, 求解出刀觸點在機床坐標系中的坐標值, 用矩陣表示為P=[X, Y, Z, 1]T。最后, 通過機床各軸的聯動使接觸輪與刀觸點保持最佳接觸狀態。那么P=Trans(Xh, Yh, Zh)×Rot(Y, B)×Rot(X, A)×P0。
因此,
 (10)
(10)
3.2 算法實現
基于上述機床, 本文對于目前的磨削運動控制算法進行了深入的研究。對于航發葉片而言, 在加工過程中, 由于應力分布不均及裝夾誤差等因素的存在, 其磨削余量極易出現分布不均勻。在相同的刀路軌跡中, 刀觸點越少, 加工效率也就越高, 故可以根據加工余量減少已經合格的刀觸點, 重新生成待加工區域, 實現加工余量的磨削加工。
對于航發葉片而言, 在磨削過程中, 磨料粒度、接觸力、砂帶線速度及葉片進給速度等磨削要素對葉片表面的去除率有著顯著影響。其中, 接觸力、砂帶線速度及葉片進給速度分別為:0~15 N, 7.5~21 m/s,17~23 mm/s。根據以上各參數的范圍, 可以得出去除量的范圍Wmin~Wmax, 從加工效率角度考慮, 以Wmax對應的磨削參數為最優。對于任一刀觸點, 如若磨削參數不變, 則磨削量為一定值, 則走刀次數為
 (11)
(11)
若ni>1, 則通過定量磨削, 使得不合格刀觸點處的加工余量Wi在0~Wmax范圍內。
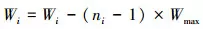 (12)
(12)
針對諸多磨削要素, 建立材料去除量的模型為
 (13)
(13)
式中:C為修正系數; Vb為砂帶線速度; Vf為葉片進給速度; Fp為接觸輪受到的壓力。
根據相關實驗數據如表 2所示, 基于正交實驗法, 得出各參數對磨削量的影響, 并獲得葉片磨削材料去除模型為
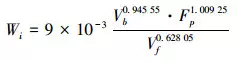 (14)
(14)
表2 某航發葉片型面磨削實驗數據
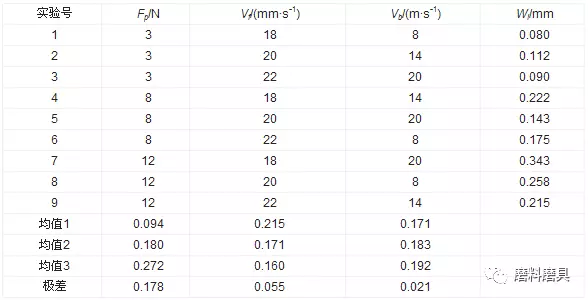
在磨削加工過程中, 一般保持砂帶線速度及葉片進給速度恒定, 在已知每個刀觸點的加工余量的基礎上, 通過調整接觸輪壓力控制材料的去除量。但是, 在磨削過程中, 第七軸施加的載荷如果幅度過大, 會嚴重影響機床的結構穩定性及磨削效果。所以本文通過調整理論模型的姿態, 優化余量分布, 從而使得加工余量盡可能均勻分布, 使得第七軸施加的載荷變化趨于平緩。
在調整理論模型姿態過程中, 主要存在6個變量:沿X, Y, Z軸的平移量Tx, Ty, Tz, 及繞X, Y, Z軸旋轉量α, β, γ。則理論模型刀觸點經過旋轉、平移變換后為
 (15)
(15)
式中:cα為cosα; sα為sinα。
此時, 在實際模型上對應點為Q′i, 加工余量W′i。
建立目標函數如下
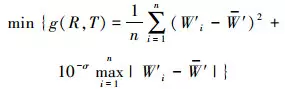 (16)
(16)
根據加工要求, 構造約束條件為
 (17)
(17)
式中:δ為局部誤差與全局誤差的數量級之差; W上偏、W下偏為加工余量上、下偏差值。
通過以上算法, 得到理論模型與實際模型余量最優位姿。并將得到的角度轉化到數控機床上, 實現磨削加工。
4 加工實驗
本實驗旨在驗證本文提出的磨削方法及其算法的正確性, 利用上述開發的軟件生成相應的數控加工代碼對航空發動機葉片進行磨削加工。另外, 為了測試本算法的準確性和有效性, 選取了其中一種加工難度較大的葉片對其磨削前后的數據進行了分析, 并與三坐標測量結果進行了對比。如圖 8所示, 某航發葉片葉身型面磨削加工實驗。針對該葉片的類型以及葉身表面的殘余量, 根據相關實驗數據制定了如表 3所示的加工參數, 磨削前后緣對比圖如圖 9所示。

圖8 某航發葉片型面磨削實驗
表3 某航發葉片實際磨削工藝參數


圖9 磨削前后緣比對圖
為了驗證本文算法的準確性以及磨削結果的可靠性, 將上述結果與三坐標測量結果進行了對比, 如表 4所示為三坐標測量的本次實驗葉片磨削前后的各截面測量結果。
表4 某航空發動機葉片磨削前后三坐標測量結果

其中, 綠色曲線表示公差帶, 紅色區域表示實測型線。由表 4中磨削前的測量結果可知, 該葉片邊緣余量分布極不均勻, 且磨削后殘余量都在公差范圍內, 其中合格區域的殘余量也并未發生太大的改變, 超差區域的殘余量也分布在+0.01 mm~+0.045 mm之間。由此可知, 本文提出的磨削方法和磨削算法能夠準確地區分合格區域和超差區域, 并能根據超差區域殘余量的不同,自動調節磨削壓力使葉身邊緣加工精度在誤差允許的范圍內。
5 結論
本文使用三坐標測量機作為測量工具, 得到了高精度航發葉片點云, 根據航發葉片曲面特征, 以非均勻有理三次B樣條曲線曲面算法擬合曲面模型, 并且測得與理論模型沿法矢方向的刀觸點處的加工余量。根據各刀觸點的加工余量,優化了加工刀路軌跡, 實現了智能磨削加工。最后進行了實際加工實驗, 機床作業過程中并沒有出現刀具長時間滯留不前及刀軸位姿突變等加工缺陷, 磨削后航發葉片前后緣粗糙度及尺寸精度均達到了實際加工要求。
參考文獻
[1] 藺小軍, 王志偉, 張新鴿, 等. 基于點搜索組合曲面清根加工軌跡優化算法[J]. 機械工程學報, 2014,50(19): 191–198
Lin X J, Wang Z W, Zhang X G, et al.Improved algorithm for clean-up machining of combinatorial-surface model basedon point-searching method[J]. Journal of Mechanical Engineering, 2014, 50(19):191–198 (in Chinese)
[2] Park S C, Chang M. Tool path generation for a surface model withdefects[J]. Computers in Industry, 2010, 61(1): 75–82DOI:10.1016/j.compind.2009.07.003
[3] Liu Z Y, Huang Y, Wei H P, et al. Research on the technology of NCabrasive belt grinding for the leading and trailing edges of aero-engineblades[J]. Advanced Materials Research, 2013, 797: 67–72 DOI:10.4028/www.scientific.net/AMR.797
[4]吳海龍. 航空發動機精鍛葉片數控砂帶磨削工藝基礎研究[D]. 重慶: 重慶大學, 2012
Wu H L. Basic research on CNC abrasive beltgrinding process of aero engine precision forged blade[D]. Chongqing:Chongqing University, 2012(in Chinese)
[5] 段繼豪, 史耀耀, 張軍峰, 等. 航空發動機葉片柔性拋光技術[J]. 航空學報, 2012,33(3): 573–578
Duan J H, Shi Y Y, Zhang J F, et al.Flexible polishing technology for blade of aviation engine[J]. Acta Aeronauticaet Astronautica Sinica, 2012, 33(3): 573–578 (in Chinese)
[6] 張明德, 王加林. 航空發動機葉片邊緣柔性拋磨技術研究[J]. 重慶理工大學學報(自然科學), 2015, 29(6): 32–36
Zhang M D, Wang J L. Research on flexiblepolishing technology for edge of aero-engine blade[J]. Journal of ChongqingInstitute of Technology (Natural Science), 2015, 29(6): 32–36 (in Chinese)
[7]劉維偉, 張定華, 史耀耀, 等. 航空發動機薄壁葉片精密數控加工技術研究[J]. 機械科學與技術, 2004, 23(3): 329–331
Liu W W, Zhang D H, Shi Y Y, et al. Studyon net-shape NC machinging technology of thin-blade of aeroengine[J].Mechanical Science and Technology, 2004, 23(3): 329–331 (in Chinese)
[8]李小彪, 史耀耀, 趙鵬兵, 等. 航空發動機葉片砂帶拋光力控制技術[J]. 計算機集成制造系統, 2012, 18(6): 1209–1214
Li X B, Shi Y Y, Zhao P B, et al. Polishingforce control technology of aero-engine blade in belt polishing[J]. ComputerIntegrated Manufacturing Systems, 2012, 18(6): 1209–1214 (in Chinese)
[9]黃云, 黃智. 砂帶磨削的發展及關鍵技術[J]. 中國機械工程, 2007,18(18): 2263–2267
Huang Y, Huang Z. Development and keytechnologies of abrasive belt grinding[J].ChinaMechanical Engineering, 2007,18(18): 2263–2267 (in Chinese) DOI:10.3321/j.issn:1004-132x.2007.18.030
[10]Sarma R, Dutta D. Tool path generation for NCgrinding[J]. International Journal of Machine Tools and Manufacture, 1998,38(3): 177–195 DOI:10.1016/S0890-6955(97)00040-0
[11]朱凱旋, 陳延君, 黃云, 等. 葉片型面砂帶磨削技術的現狀和發展趨勢[J]. 航空制造技術, 2007: 102–104
Zhu K X, Chen Y J, Huang Y, et al. Presentstatus and development trend of abrasive belt grinding technique for bladeprofile[J]. Aeronautical Manufacturing Technology, 2007: 102–104 (inChinese)
[12]劉樹生, 楊建中. 葉片六軸聯動數控砂帶磨床與數控砂帶磨削單元化[J]. 航空制造技術, 2010:32–37
Liu S S, Yang J Z. 6-Axis hybrid NCbelt-grinding machine for blade and unitization of NC belt-grinding[J].Aeronautical Manufacturing Technology, 2010: 32–37 (in Chinese)
[13]朱心雄. 自由曲線曲面造型技術[M]. 北京: 科學出版社, 2000: 152-330
Zhu X X. Free curve and surface modelingtechnology[M]. Beijing:Science Press, 2000: 152-330 (in Chinese)
[14]何雪明, 孔麗娟, 何俊飛, 等. 基于三坐標測量機自適應測量的自由曲面逆向[J]. 機械工程學報, 2014, 50(15): 155–159
He X M, Kong L J, He J F, et al. Free-formsurface reverse based on CMM self-adapting measurement[J]. Journal ofMechanical Engineering, 2014, 50(15): 155–159 (in Chinese)
[15] Loney G C, Ozsoy T M. NC machining of free form surfaces[J].Computer-Aided Design, 1987, 19(2): 85–90DOI:10.1016/S0010-4485(87)80050-7
本文刊登于《機械科學與技術》2018年第37卷5期


 手機資訊
手機資訊 官方微信
官方微信








 豫公網安備41019702003604號
豫公網安備41019702003604號